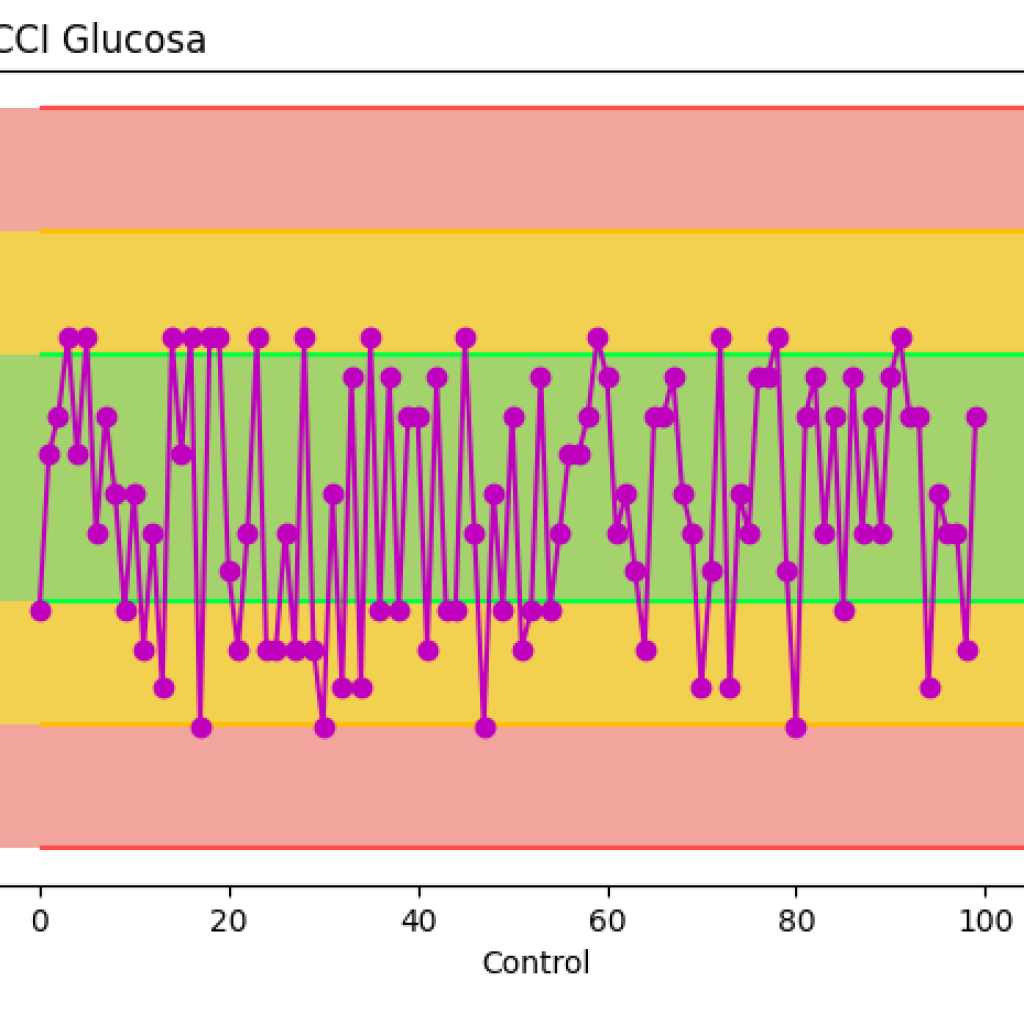
Grafico de Control (Levey Jennings) con Python
En esta guía revisaremos los pasos a seguir para la confección de un Gráfico de Control (Levey & Jennings) utilizando Python como lenguaje de Programación y Google Colaboratory como entorno de Interpretación de Python,
P1.- Paso Inicial, los datos…
Para comenzar debemos identificar los valores que corresponden a nuestro control y de estos tomar los primeros 20 valores como nuestro N20 para el gráfico correspondiente, los controles los colocamos en una hoja de Cálculo en la columna A y exportamos esta hoja con el formato Texto separado por Comas (*.CSV)
P2.- Google Colab
Ingresamos a Google Drive y creamos un archivo de Google Colaboratory, este tendrá una extensión ipynb y por lo tanto es un archivo Python Notebook
P3.- Carga de Librerías
Insertamos un segmento de Código en nuestro colab y copiamos el siguiente código
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import io
from google.colab import files
uploaded = files.upload()
P4.- Corremos el segmento de Código antes copiado y subimos nuestro archivo CSV, que contiene los datos del Control.

P5.- Convertimos el archivo CSV en un Dataframe almacenado en la variable df
NOTA: Muy importante reemplazar el nombre del archivo por el que corresponde a nuestro archivo antes enviado a nuestro entorno Colab
NOTA2: Importante es colocar como variable sep, el separador de listas que tiene nuestro CSV, recordemos que el formato USA de separador es la coma, pero en Latinoamérica se utiliza punto y coma ; esto puede afectar nuestra importación
df = pd.read_csv(io.BytesIO(uploaded[‘ControlGlucosa100.csv’]),sep=»;»)
df
P6.- Ahora convertimos los primeros 20 datos de la columna del Dataframe que contiene los controles en una lista con el nombre controlGlucosa, para esto utilizamos la función .tolist()
controlGlucosa = df.head(20)[‘Glucosa’].tolist()
controlGlucosa
El nombre de la columna que contiene los datos de control debe ser colocado entre comillas simples o en su defecto el indicede la misma, recordemos que en Python partimos desde el número 0
P7.- Test de Dixon
Para realizar el test de Dixon en primer lugar creamos un segmento de código para definir 3 variables que contendrán las listas de valores de tabla para el contraste del test de Dixon.
q90 = [0.941, 0.765, 0.642, 0.56, 0.507, 0.468, 0.437,
0.412, 0.392, 0.376, 0.361, 0.349, 0.338, 0.329,
0.32, 0.313, 0.306, 0.3, 0.295, 0.29, 0.285, 0.281,
0.277, 0.273, 0.269, 0.266, 0.263, 0.26
]
q95 = [0.97, 0.829, 0.71, 0.625, 0.568, 0.526, 0.493, 0.466,
0.444, 0.426, 0.41, 0.396, 0.384, 0.374, 0.365, 0.356,
0.349, 0.342, 0.337, 0.331, 0.326, 0.321, 0.317, 0.312,
0.308, 0.305, 0.301, 0.29
]
q99 = [0.994, 0.926, 0.821, 0.74, 0.68, 0.634, 0.598, 0.568,
0.542, 0.522, 0.503, 0.488, 0.475, 0.463, 0.452, 0.442,
0.433, 0.425, 0.418, 0.411, 0.404, 0.399, 0.393, 0.388,
0.384, 0.38, 0.376, 0.372
]
Q90 = {n:q for n,q in zip(range(3,len(q90)+1), q90)}
Q95 = {n:q for n,q in zip(range(3,len(q95)+1), q95)}Q99 = {n:q for n,q in zip(range(3,len(q99)+1), q99)}
Luego colocamos otro segmento de código con la función de dixon_test
def dixon_test(data, left=True, right=True, q_dict=Q95):
«»»
Keyword arguments:
data = A ordered or unordered list of data points (int or float).
left = Q-test of minimum value in the ordered list if True.
right = Q-test of maximum value in the ordered list if True.
q_dict = A dictionary of Q-values for a given confidence level,
where the dict. keys are sample sizes N, and the associated values
are the corresponding critical Q values. E.g.,
{3: 0.97, 4: 0.829, 5: 0.71, 6: 0.625, …}
Returns a list of 2 values for the outliers, or None.
E.g.,
for [1,1,1] -> [None, None]
for [5,1,1] -> [None, 5]
for [5,1,5] -> [1, None]
«»»
assert(left or right), ‘At least one of the variables, `left` or `right`, must be True.’
assert(len(data) >= 3), ‘At least 3 data points are required’
assert(len(data) <= max(q_dict.keys())), ‘Sample size too large’
sdata = sorted(data)
Q_mindiff, Q_maxdiff = (0,0), (0,0)
if left:
Q_min = (sdata[1] – sdata[0])
try:
Q_min /= (sdata[-1] – sdata[0])
except ZeroDivisionError:
pass
Q_mindiff = (Q_min – q_dict[len(data)], sdata[0])
if right:
Q_max = abs((sdata[-2] – sdata[-1]))
try:
Q_max /= abs((sdata[0] – sdata[-1]))
except ZeroDivisionError:
pass
Q_maxdiff = (Q_max – q_dict[len(data)], sdata[-1])
if not Q_mindiff[0] > 0 and not Q_maxdiff[0] > 0:
outliers = [None, None]
elif Q_mindiff[0] == Q_maxdiff[0]:
outliers = [Q_mindiff[1], Q_maxdiff[1]]
elif Q_mindiff[0] > Q_maxdiff[0]:
outliers = [Q_mindiff[1], None]
else:
outliers = [None, Q_maxdiff[1]] return outliers
P8 Ahora evaluamos el valor Menor y Mayor por medio de la función dixon_test
dixon_test(controlglucosa)
El resultado lo observamos como una lista con el resultado de la evaluación, en primer lugar la evaluación del menor menor y luego el Mayor
[None, None]P9 Quitamos los outliers si es que el test de dixon nos indica su presencia
P10 Es tiempo de identificar algunos estadigrafos propios de nuestro control, como El valor Menor, Mayor, la Media, la Desviación estándar y el Coeficiente de Variación
El siguiente código nos ofrece todos los estadigrafos de controlList
def mayor(lista):
max = lista[0];
for x in lista:
if x > max:
max = x
return max
def menor(lista):
min = lista[0];
for x in lista:
if x < min:
min = x
return min
# Identificamos el Valor Menor
vmenor=menor(controlGlucosa)
vm = f’Valor Menor {vmenor}’
print(vm)
# Identificamos el Valor Mayor
vmayor=mayor(controlGlucosa)
vm = f’Valor Mayor {vmayor}’
print(vm)
# Calculamos la Media de controlList
media = float(np.mean(controlGlucosa))
MED = f’Media: {media}’
print(MED)
# Calculamos la SD de controlList
sd = float(np.std(controlGlucosa))
SD = f’SD: {sd}’
print(SD)
# Calculamos el CV de controlList
cv = (sd / media)*100
CV = f’CV: {cv}’
print(CV)

P11 Para la construcción del gráfico de control ahora calculemos los límites de la media +/- 1, 2 y 3 DS
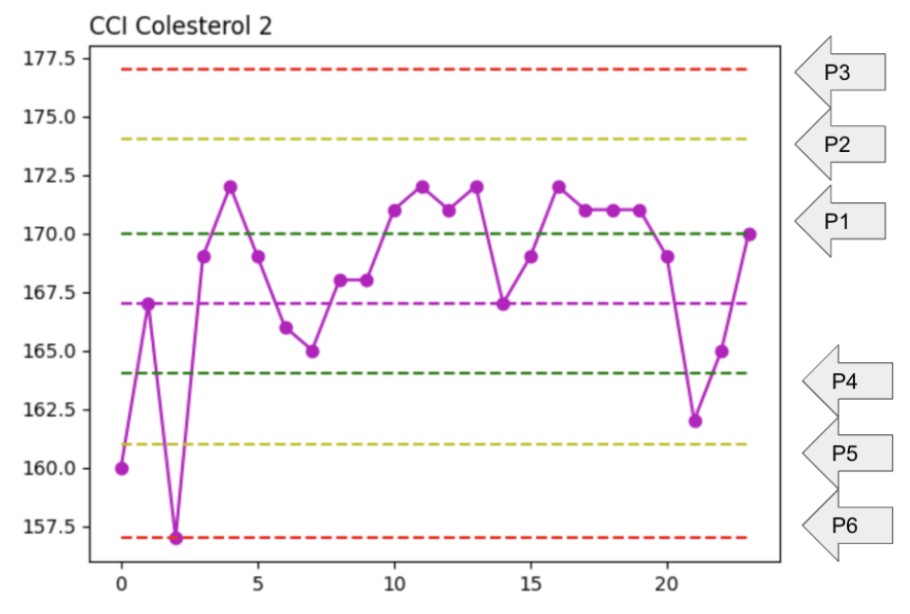
este código nos permite identificarlos como P1, P2, P3, P4,P5 y P6
P1 = media + sd
P2 = media + (sd*2)
P3 = media + (sd*3)
P4 = media – sd
P5 = media – (sd*2)
P6 = media – (sd*3)
print(f’P1: {P1}’)
print(f’P2: {P2}’)
print(f’P3: {P3}’)
print(f’P4: {P4}’)
print(f’P5: {P5}’)

P12 y ahora el paso final…. Graficamos !!!
from pylab import *
import matplotlib.pyplot as plt
plt.title(«CCI Colesterol», loc = ‘left’)
plt.xlabel(«Control»)
plt.ylabel(«»)
plt.plot(df[‘ Control ‘], «mo-«,label=»Control»)
plt.plot(df[‘ Media ‘],»m–«, label=»Media»)
plt.plot(df[‘ sd ‘],»g–«,label=»1SD»)
plt.plot(df[‘ menossd ‘],»g–«,label=»-1SD»)
plt.plot(df[‘ dossd ‘],»y–«,label=»2SD»)
plt.plot(df[‘ menosdossd ‘],»y–«,label=»-2SD»)
plt.plot(df[‘ tressd ‘],»r–«,label=»3SD»)
plt.plot(df[‘ menostressd ‘],»r–«,label=»-3SD»)
plt.axhspan(P3, P6, facecolor=’#E74C3C’, alpha=0.5)
plt.axhspan(P2, P5, facecolor=’#F2FE05′, alpha=0.5)
plt.axhspan(P1, P4, facecolor=’#58D68D’, alpha=0.5)
plt.show()